对于母串X=x1,x2,⋯,xm , Y=y1,y2,⋯,yn,求LCS与最长公共子串。
暴力解法
假设 m<n, 对于母串X,我们可以暴力找出2的m次方个子序列,然后依次在母串Y中匹配,算法的时间复杂度会达到指数级O(n∗2的m次)。显然,暴力求解不太适用于此类问题。
动态规划
假设Z=z1,z2,⋯, zk是X与Y的LCS, 我们观察到
如果Xm=Yn,则Zk=Xm=Yn,有Zk−1是Xm−1与Yn−1的LCS;
如果Xm≠Yn,则Zk是Xm与Yn−1的LCS,或者是Xm−1与Yn的LCS。
所以如果用一个二维数组c表示字符串X和Y中对应的前 i,前 j个字符的LCS的长度话,可以得到以下公式:
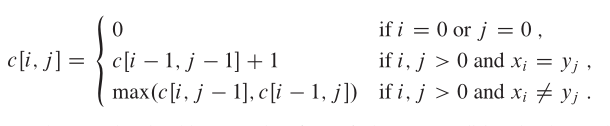
DP求解LCS
因此,我们只需要从c[0][0]开始填表,填到c[m-1][n-1],所得到的c[m-1][n-1]就是LCS的长度
用二维数组c[i][j] 记录串x1x2⋯xi与y1y2⋯yj的LCS长度,则可得到状态转移方程
例如,设所给的两个序列为X=”A,B,C,B,D,A,B”和Y=”B,D,C,A,B,A”。由算法LCS_LENGTH和LCS计算出的结果如下图所示:
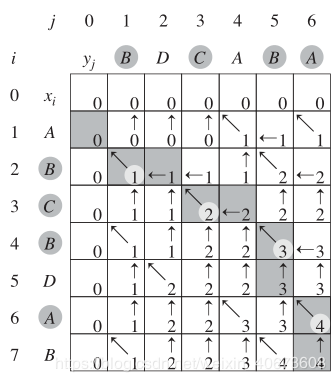
如上图 ,两层循环 , 先循环 X , 里层循环 Y, 遇到相等那子序长度就会加1,那前一个子序长度是 c[i -1][j-1], 如果比较不想等, 子序长度就不增加, 当前子序长度 就是c[i-1][j] 或c[i][j-1] 其中大的值. 如上图不相等时,当前的数子会取 上边或左边 最大数子。 遍历完就能得到 子序长度 c[6][7]
若想得到LCS,则再遍历一次b数组就好了,从最后一个位置开始往前遍历:
- 如果箭头是↖,则代表这个字符是LCS的一员,存下来后 i– , j–
- 如果箭头是←,则代表这个字符不是LCS的一员,j–
- 如果箭头是↑ ,也代表这个字符不是LCS的一员,i–
- 如此直到i = 0或者j = 0时停止,最后存下来的字符就是所有的LCS字符
function lcs( str1, str2) {
var len1 = str1.length;
var len2 = str2.length;
var c = [...new Array(len1 + 1).keys()].map(v => []);
// or v => new Array(len2 +1)
/* [
[...],
[...]
...
] */
var z;
for (var i = 0; i <= len1; i++) {
for( var j = 0; j <= len2; j++) {
if(i == 0 || j == 0) {
c[i][j] = 0;
} else if (str1.charAt(i-1) == str2.charAt(j-1)) {
c[i][j] = c[i-1][j-1] + 1;
} else {
c[i][j] = Math.max(c[i - 1][j], c[i][j - 1]);
}
}
}
console.log(c[len1][len2]); // 最长子序长度
return c;// 二维数组表,数组最后一位 c[n-1][m-1] 就是长度m n是二维数组长度
}
//最长子序 是什么
function llcs(dp, len1, len2){
var i, j, z = 0;
var c = [];
i = len1, j = len2;
while(i!=0 && j!=0) {
if(a[i-1] == b[j-1]) { // 相等代表这个字符是LCS的一员
c[z++] = a[--i];
j--;
} else if(dp[i-1][j] < dp[i][j-1]) {
//如果 j-1 数字大, 这个子序长 ,从这条检索,然后j - 1
j--;
}else if(dp[i][j-1] <= dp[i-1][j]) {
// 如果 i -1 大 , 从 i-1 检索
i--;
}
}
console.log(c);
}
var a = 'abdejfsapfaasg3sadfp3f';
var b = 'asf3fahfpjasdfjiuegiada';
llcs(lcs(a,b),a.length,b.length );